In the last episode of this mini-series I explained about how an assembler’s job is effectively to convert a program written in a language a human programmer can understand (assembly language in this case) into something which a computer can understand. So as an example, the assembler will take something like this …
start: ldi a,1 ; initial setup A = 1
ldi b,0 ; B = 0
loop: mov c,b ; slide B -> C
mov b,a ; A -> B
add ; and add together
done: bcs done ; infinite loop if overflowed
jmp loop ; otherwise have another go
… and turn it in to something like this …
41
60
11
08
81
E8 00 05
E6 00 02
In the last episode I also walked through the steps required to ‘hand assemble’ the program above but what we’re interested in is how to make a computer read and understand our assembly program and convert it in to the ‘machine code’ seen above. In other words, how do we start to write our assembler?
So first of all let’s take a look again at that assembly program at the top of this page … what do you see? Well, there’s a lot comes for free with the human brain and, for me, I’m automatically extracting a lot of semantic meaning out of what really is just a series of characters - a file of text. That is, to the assembler, the program is going to look something more like this:
start: ldi a,1 ; initial setup A = 1\n ldi b,0 ; B = 0\n\nloop: mov c,b ; slide B -> C\n mov b,a ; A -> B\n add ; and add together\n\ndone: bcs done ; infinite loop if overflowed\n\n jmp loop ; otherwise have another go
The first job of an assembler is to take the stream of characters above and try and derive some sort of meaning from it. A good place to start here is to try and break it down in to tokens, i.e. try and group sets of characters together to form pieces that have some meaning. This is a process called tokenisation or lexical scanning.
In the simplest case we can go one character at a time and when we have something we recognise we can create a token … so for example:
s
st
sta
star
start
start:
By the time we’ve considered the first 6 characters of the input we’ve recognised that this must be a label because it contains
one or more letters followed by a single :. By building up a series of these ‘rules’ we can build our tokeniser.
Let’s start with some easy bits:
WSS = WS+
WS = ' ' / '\t'
What now?! Yes, well, I appear to have introduced yet another language … this time it’s a derivative of a parsing expression grammar, that is, a language designed to define the syntax and grammar of a language.
Let’s break down what’s going on … if we look at the second line I’m defining a token called WS that can be a single
space character or a single tab character \t. In other words it’s all the characters that we would consider being
white space.
Above that line we define another token called WSS and that consists of one or more instance of WS (that’s what the +
represents). This will ensure that any sequence of whitespace characters is considered a single WSS token.
So, what does this give us. Well, lets tokenise the first two lines our original program:
start: ldi a,1 ; initial setup A = 1
ldi b,0 ; B = 0
… becomes …
[
"start:", "WSS", "ldi", "WSS", "a,1", "WSS", ";", "WSS", "initial", "WSS", "setup", "WSS", "A", "WSS", "=", "WSS", "1",
"WSS", "ldi", "WSS", "b,0", "WSS", ";", "WSS", "B", "WSS", "=", "WSS", "0"
]
For the purposes of clarity I’ll ignore the WSS tokens from this point forward but just remember they’re still valid tokens
and would be included in the result of our tokenisation process. With WSS excluded we get:
[
"start:", "ldi", "a,1", ";", "initial", "setup", "A", "=", "1",
"ldi", "b,0", ";", "B", "=", "0"
]
We’ve now captured all of the white space now but are left with groups of characters that still have no meaning. Where next?
Well, one thing that stands out is the comments - effectively everything on a single line after a semicolon ;.
These are there purely for the benefit of the human programmer and have no meaning or use for the assembler or for the
resulting machine code that’ll be used by the relay computer. Let’s get that defined and added to our tokeniser:
COMMENT = (SEM (!EOL .)*)
EOL = [\n\r]
SEM = ';'
So, this one’s a bit more complex but let’s take it a bit at a time. Firstly I define SEM to be the single semicolon character
of ;. Likewise I define EOL to be characters representing the end of a line. These are hidden in a text editor but if you
looked at the stream of characters in the file you’d see a \n or a \r or maybe even a combination of both. This does
differ between Linux, Mac and PCs and has caught many a programmer out over the years. The square brackets here though say the
character we’re checking against can be any one of the items within the square brackets.
We now get to the complex part … the COMMENT definition. A comment always starts with a SEM (semicolon) and can then be
followed by any number (represented by the *) of any character (represented by the .) providing it’s not (represented by
the !) an EOL (end of line) type character.
Detecting comments in some languages can be a lot more involved and many languages allow comments over multiple lines. For
example, C# treats everything between /* and */ as a comment. Here in our assembly language we keep it simple and everything
after a ; will be ignored right up until the end of the line. So, what does that do for our tokenising:
start: ldi a,1 ; initial setup A = 1
ldi b,0 ; B = 0
… becomes …
[
"start:", "ldi", "a,1", "COMMENT",
"ldi", "b,0", "COMMENT"
]
That’s looking much better and we’ve effectively removed things we’re not really interested in which means the text that remains is our actual program that has the real meaning that we’ll need to handle.
The most important meaning in our program is the assembly language mnemonics (the three letter instructions that tell the
computer what type of action to perform). In our full assembly program above we have ldi, mov, add and so on. These are
pretty straightforward to pick out:
MNEMONIC = [a-z]i+
So, this says that any one character between a and z is acceptable and then we follow that with an i (meaning we’re not
worried about case and ldi is the same as LDI … and even LdI is ok) and then finally, as before, the + says we’ll
want one or more of these ‘acceptable characters’ in a sequence. That now gives us:
[
"MNEMONIC(start)", ":", "MNEMONIC(ldi)", "MNEMONIC(a)", ",1", "COMMENT",
"MNEMONIC(ldi)", "MNEMONIC(b)", ",0", "COMMENT"
]
Oh dear, what’s gone wrong there then?! Well, this is an example of a tokenising rule being ‘greedy’. It’s recognised things it shouldn’t have and mis-categorised them because our rules aren’t specific enough.
What can we do to improve this? Well, let’s look at what’s been mis-identified … the a in a,1 and the b in b,0 stand
out and that’s because although they’re using letters just like the mnemonics we’re actually referring to registers here. Let’s
define this rule alongside the MNEMONIC rule:
MNEMONIC = [a-z]i+
REGISTER = (A / B / C / D)
A = 'a'i
B = 'b'i
C = 'c'i
D = 'd'i
This maybe looks more complicated than it really is. For convenience we define A, B, C and D to represent the
characters a, b, c and d respectively. Note for each I’ve added i to indicate we’re case insensitive and so a or A
are both an A token. So, with that in hand a REGISTER is a single A, B, C or D token. Let’s see what that does for
our tokenising:
[
"MNEMONIC(start)", ":", "MNEMONIC(ldi)", "REGISTER(a)", ",1", "COMMENT",
"MNEMONIC(ldi)", "REGISTER(b)", ",0", "COMMENT"
]
We can likewise fix the mis-identified start: label by defining how we know when something is a label:
LABEL = ident COL
ident = (alpha+ alphanum*)
alpha = [a-zA-Z_]
alphanum = [a-zA-Z_0-9]
COL = ':'
So, a LABEL is an ident followed by a colon : and an ident is one or more alpha characters followed by zero
or more alphanum characters, that is, an identifier can be made up of letters or numbers but must start with a letter.
The * indicates zero or more here whereas the + indicates one or more. With this rule we’re now at:
[
"LABEL(start:)", "MNEMONIC(ldi)", "REGISTER(a)", ",1", "COMMENT",
"MNEMONIC(ldi)", "REGISTER(b)", ",0", "COMMENT"
]
Keeping up? Effectively though this whole process is about defining the rules needed to extract the tokens from the plain text.
Finishing off we can pick out the literal values 0 and 1 along with the , as follows:
LITERAL = decimal
COMMA = CMA
decimal = [0-9]+
CMA = ','
… to get …
[
"LABEL(start:)", "MNEMONIC(ldi)", "REGISTER(a)", "COMMA", "LITERAL(1)", "COMMENT",
"MNEMONIC(ldi)", "REGISTER(b)", "COMMA", "LITERAL(0)", "COMMENT"
]
… and with that we’ve extracted a list of tokens from our original stream of characters and that’s pretty much it for the first process in assembling an assembly language program.
Now we’ve got our list of tokens we need to extract some sort of semantic meaning from them, that is, what are these series of tokens actually asking us to do and does that actually make sense? Is it something the computer is actually capable of doing? This we’ll look at in the next episode of this mini-series.
The definition language I’ve been using so far is utilised by PEG.js to create a tokeniser (and a parser too as we’ll see in the next episode) taking all the hard work out of this stage of the assembly process. You could, of course, create a tokeniser from scratch but there really is no need with something like PEG.js.
If you’d like to have a play with tokenising you can use the PEG.js online tool here. The full tokeniser covered so far is below and you can enter this in the left-hand pane and then put the assembly program from the top of this post in the right hand pane. The result will be the tokenised output at the bottom right.
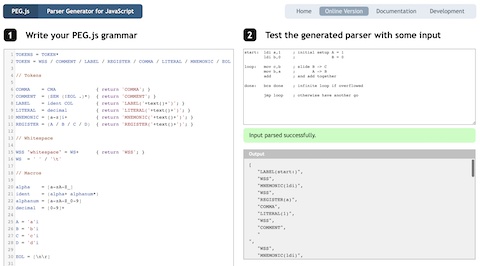
TOKENS = TOKEN*
TOKEN = WSS / COMMENT / LABEL / REGISTER / COMMA / LITERAL / MNEMONIC / EOL
// Tokens
COMMA = CMA { return 'COMMA'; }
COMMENT = (SEM (!EOL .)*) { return 'COMMENT'; }
LABEL = ident COL { return 'LABEL('+text()+')'; }
LITERAL = decimal { return 'LITERAL('+text()+')'; }
MNEMONIC = [a-z]i+ { return 'MNEMONIC('+text()+')'; }
REGISTER = (A / B / C / D) { return 'REGISTER('+text()+')'; }
// Whitespace
WSS "whitespace" = WS+ { return 'WSS'; }
WS = ' ' / '\t'
// Macros
alpha = [a-zA-Z_]
ident = (alpha+ alphanum*)
alphanum = [a-zA-Z_0-9]
decimal = [0-9]+
A = 'a'i
B = 'b'i
C = 'c'i
D = 'd'i
EOL = [\n\r]
CMA = ','
COL = ':'
SEM = ';'